连续声波振幅的封闭容器外液位测量理论与计算方法

1、概述：
    本研究提出了一种基于连续声波振幅的外源液位测量方法。通过构建15个多高斯光束叠加模型，分析了圆形活塞液位计液位计液位计传感器在金属固体声场中的分布; 根据超声波的反射和折射特性，计算出回声压力的计算方法。三幅振幅的连续波被用作超声波液位计液位计液位计传感器的驱动源，采用两个直径相同的单晶液位计液位计传感器作为超声波发射端子和接收端子，对四组不同壁厚的容器进行实验，并比较三种振幅的驱动源回波能量特征。低于不同壁厚的液位。两组不同直径的液位计液位计传感器用于测量实验模型的液位，并分析和比较两组液位计液位计传感器的测量误差。实验结果表明，该模型的测量误差小于5 mm，适用于多个领域的液体或液体混合物的液位测量。两组不同直径的液位计液位计传感器用于测量实验模型的液位，并分析和比较两组液位计液位计传感器的测量误差。实验结果表明，该模型的测量误差小于5 mm，适用于多个领域的液体或液体混合物的液位测量。两组不同直径的液位计液位计传感器用于测量实验模型的液位，并分析和比较两组液位计液位计传感器的测量误差。实验结果表明，该模型的测量误差小于5 mm，适用于多个领域的液体或液体混合物的液位测量。

简介： 
    在放养罐和其它容器材料的高度和体积测量通常采取在化工，食品的存储和石油在生产过程中，以确保材料供给的[ 1，2 ]。
    影响测量精度的因素是将被认为是在容器的密封介质，腐蚀性物质，毒性和爆炸性的材料[ 3，4 ]。为了满足各种影响因素的要求，开发了液位液位计液位计传感器。目前，商业液位测量包括雷达，超声波，同位素或放射性，电子，热学，光学仪表和液压计。虽然达到成功的应用，它们必须被直接设置与液体连接容器，或在需要的声波和电磁波[ 5，6 ]。
    石油，化工，能源，航空航天和其他行业的特殊申请人条件要求专门的液位测量和设备。对于易燃物和爆炸物的条件，超低温，高压等液体的应用特性，储存应安置在大型，密闭容器和低温，高压环境中远离电，磁，碰撞，和其他危险部位，对水平测量方法和原理提出了更高的要求。
    鉴于这些方法的优点和缺点，本研究提出了一种检测模型，用于确定基于连续声波振幅的密封容器外部的液位，并且所提出的方法不需要在容器中安装液位计液位计传感器或设备。提前，也没有损坏容器[的物理结构和完整性7，8 ]。
    本研究使用多元高斯声束模型来模拟容器壁辐射声场中的圆形活塞式换能器。根据光束传播的形状和传播特性，分析了不同曲率的容器壁对辐射场的影响。根据容器中气体和液体介质的超声波阻抗差异，回波声压计算模型，建立了与连续的声音波振幅[ 9，10，11，12 ]。
    如图1所示，R wg表示液面上方内表面的反射系数; R wl指的是低于液位的反射系数。当液位计液位计传感器分别位于液面上方和下方时，由于不同的阻抗，内表面处的反射系数R wg和R wl不相等，这使得与所接收的回波相关的声压不同。然后在液位以上的临界点处，回波声压保持恒定，并且液位下方有一个点。因此，检测中声压的变化特性用于测量液位。

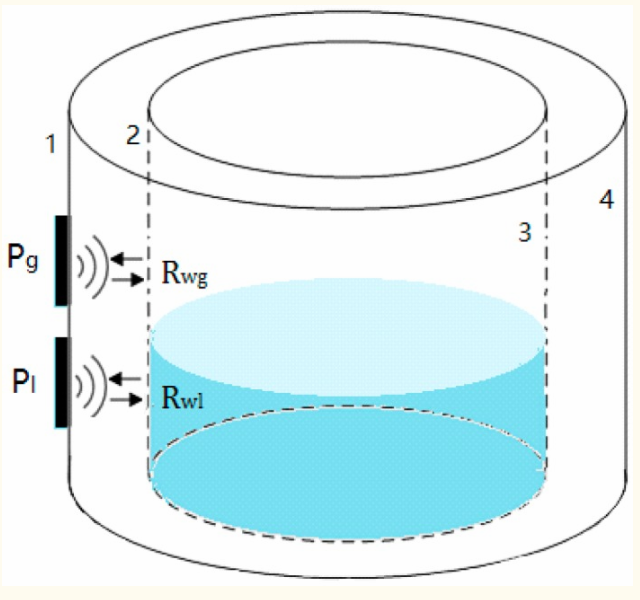
2、理论与方法

固体圆形活塞液位计液位计传感器的声场
  在高斯波束叠加的十五个多变量模型中[ 13 ]，固体样本中任意点（x 2，y 2，z 2）的声压大小可表示为（1）

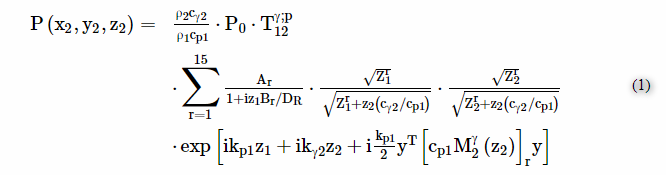
    其中A r和B r是多元高斯光束的叠加系数，?γ ; p12是平面波传播系数。参数D R = k p1 a 2/2是瑞利距离，a是换能器的半径，k p1是介质1中P波的波数。类似地，kγ2（α= p，s）是介质2中的P波或S波的波数。Z 1是第一介质中测试声束的行程长度; Z 2是第二介质中的长度。P 0是初始入射声压。ρ 1，ρ 2是介质密度，C P1是在液体中的纵波的波速度，C γ2 是固件样本中的纵向或剪切波速度。 中号γ2 是与超声波束的入射角和界面的曲率相关的2×2矩阵。

为了进一步讨论，该等式被简化为

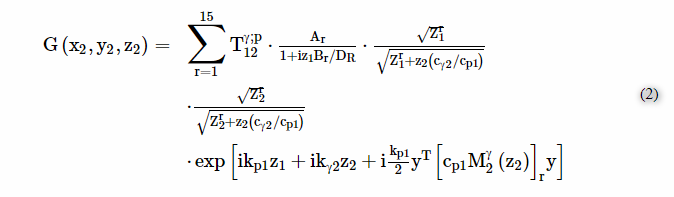
图2示出了由15高斯声束叠加的声场的三维视图。在图2中，a和b表示圆形活塞探针在金属铝中的声场分布。压缩波速度为6300m / s，剪切波速度为3100m / s，超声波阻抗为17×105gm / cm 2 ·s。

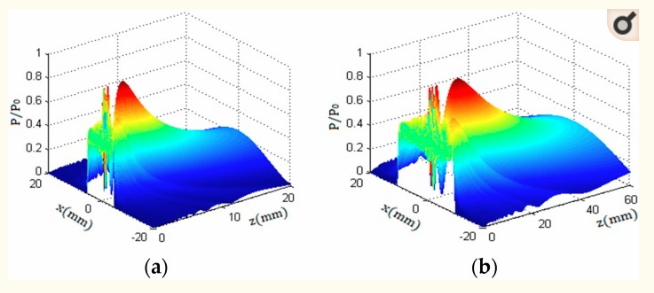
通过对声场分布理论的分析和3D视图的图2，我们知道圆形活塞液位计液位计传感器的声场由近场和远场两部分组成; 并且近场有很多较大和较小声压。在远场，声压随着传播距离的增加而逐渐减小。由于圆形液位计液位计传感器的声场沿其轴线是对称的，因此可以沿着波束的传播方向获得波束的任何横截面的声压分布特性[ 14 ]。

然后近场光束保持圆柱传播，几乎没有发散; 远场光束以漫射方式扩散，具有一定的漫射角。由N个被给予近场N和扩散角α的长度=α 2 /λ ?和α=反正弦（1.22λ ? / 2a）中，分别，其中λ ?是在金属壁的超声波的波长， a是液位计液位计传感器的半径[ 15 ]。

从上述分析可以推断，沿着声束的传播方向，超声波束的任何横截面都在圆形区域中。因此，当声束在传播距离之后到达容器的内表面时，投影是圆形截面，其中光束能量主要集中。我们将投影圆称为能量圆，其直径用d表示，d的值可以用公式（3）计算：

计算回声声压
由于高斯声束是垂直于平面的界面，其反射和透射特性遵循平面波[传播16，17 ]。因此，反射系数计算如下：

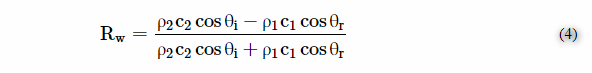
其中c 1，c 2是介质中声速，θi是入射角，θr是反射角。

如图3所示，假设容器的壁厚为L; 液位计液位计传感器的半径是a; 通过将圆形液位计液位计传感器的中心O作为坐标原点来建立坐标系。根据多元高斯光束模型，让z 1 = 0，z 2 = L，由圆形液位计液位计液位计传感器在容器内壁上的任何点p（x 2，y 2，z 2）发射的超声压力P L.壁厚L可以表示为

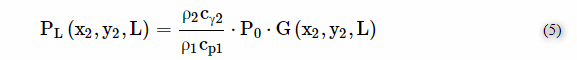
根据以上对能量圆的分析，将直径为d的圆形梁截面中的声压积分; 假设能量圆的总面积由能量圈表示，并且能量圈中的平均声压获得如下：
 

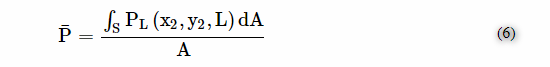
根据声学的基本知识，超声波在具有不连续阻抗的界面处被折射和反射，其遵循平面声波的折射和反射原理。假设容器内壁的平均反射回声声压为p[Rˉˉˉ， 然后
 

在实际检测中，当液位计液位计液位计传感器沿着壁的外表面向上移动并且能量圆的顶部超过液位时，多余的高度由Δd（0≤Δd≤d）表示，即液位以上的区域表示为A e，令r s = A e / A.

当0≤Δd≤d时，“能量圆”由液位分为两部分，声能阻抗在能量圆的两个部分不再相等，这将导致两部分的声学边界条件也不同。因此，它由两部分计算，并代表能量圈两部分的反射系数; 液位计液位计液位计传感器接收的回声声压应由能量圈的两个部分叠加。

我们假设在n次之后，墙壁中的反射回波将衰减到非常小的量，这相对于接收液位计液位计液位计传感器接收的总能量可以忽略不计。

因此，当声束在n次后返回到墙壁的外表面时，液位计液位计液位计传感器的总声压通过以下等式导出：
 

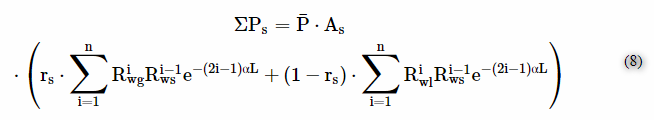
其中，容器壁处的超声衰减系数代表液位计液位计液位计传感器表面反射系数。

3.实验结果

系统安装和初始条件
图4显示了实验系统的组成。
 

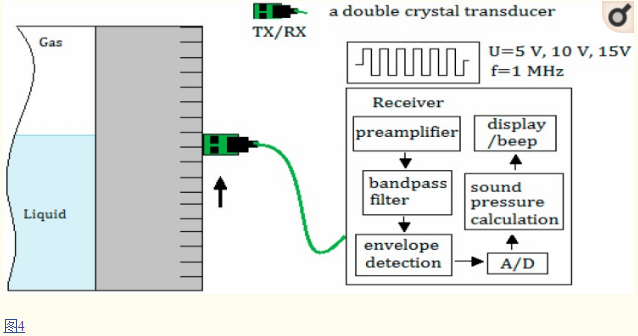
在实验中使用四组不同壁厚，8mm，25mm，40mm和50mm的容器进行测量; 容器的物质是铝合金，液体作为容器中的液体介质，大气作为气体介质。表1中的参数显示金属容器Z m的阻抗，容器Z l中液体介质的阻抗，容器中气体介质的阻抗Z g，内壁与气体R wg之间的反射系数，反射内壁和液体R wl之间的系数，以及外壁和探针R ws之间的反射系数。
 

驱动源设计为连续波振幅激励，即连续波的振幅在5V，10V和15V的三个周期中依次进行，以驱动探头发射不同振幅的超声波。由于使用连续波激发，超声换能器与双晶探头一起使用，一个用于发射，一个用于接收，并且两者都具有10mm的直径和50mm的焦距。

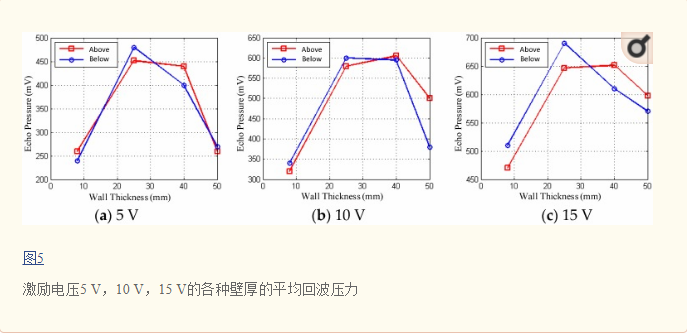
如图5所示，对于不同的幅度激励信号值，在液位之上和之下的回波能量的两个临界值之间的差异在给定的测试环境中显示出不同的特性。在表2中，当在容器壁厚的所有区域中激活三个幅度电压信号时，始终存在一组与厚壁匹配的激励电压值，并且液体水平低于两个临界值的回波能量差异是更高的分辨率，明确的区别，这为判断液位确定提供了依据。
 

回声声压计算
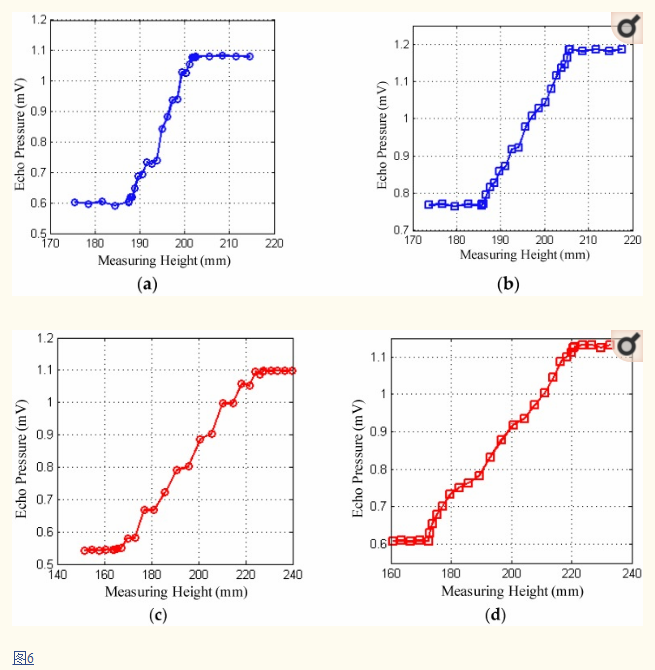
图6示出了针对不同壁厚的不同尺寸的探针的实际测量值，横坐标表示探针沿容器外壁测量的高度，纵坐标表示接收探针接收的回波压力的幅度。超声回波由接收电路接收。对回波信号的增益进行放大，滤波，检测以进行数据处理，并转换为相应的电压幅度显示输出。在该图中，激励电压设定为15V，例如壁厚为L = 8mm且L = 50mm。
 

水平测量结果
图7显示了使用第3节中的理论模型进行液位测试的真实结果。容器中的液位为水，实际液位为200毫米。在该实验中，使用直径为15mm和20mm的两种不同尺寸的换能器来测量壁厚L分别为8mm，25mm，40mm和50mm的液位。Pˉ较大 和 Pˉ分表（表3）中的回声声压值分别在上下临界位置测得，h l是实际的液位值，Hˉ较大 和 Hˉ分 分别是液位的上下临界位置的高度。 Hˉ米 是实际的测量结果，和 ||Δ èˉˉˉˉˉ||是测量的平均误差。表中的所有测量值均为三次实验的平均值。
 

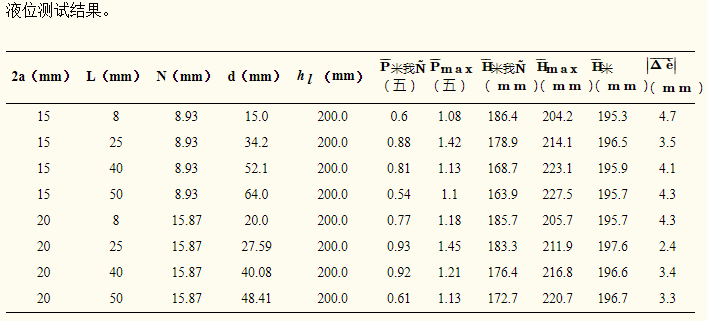
图7a示出了能量圆的直径d与由不同壁厚的两个不同直径的探针产生的梁的壁厚L之间的对应关系。在该图中，直径为15mm的换能器随着传播距离的增加而更快地发射超声波束发散。在相同的壁厚下，能量圆的直径d线性增加，这表明光束快速扩散，声束在相应能量圆的单位面积内的能量也减小，即平均声压光束减小会影响检测分辨率。由直径为20mm的换能器产生的光束发散相对平坦。

图 7b示出了在两个关键位置处由探头的两个不同直径接收的回声声压与在不同壁厚下的壁厚L之间的对应关系。不同壁厚的两种不同直径的探头显示出相同的变化。壁厚为40 mm时，压差变得较小。壁厚为25mm和50mm时，压差变大。这对于测量水平和提高测量分辨率非常有用。在壁厚为8mm时，由于在探头和容器壁之间使用延迟块，在上下临界位置处的压降也更明显。

从图7中还可以看出b，当使用小直径探针时，不同壁厚的两个临界位置处的回波压力之间的差异通常高于较大直径探针。随着换能器直径的增加，超声波束将变得更加聚焦，发散角变小，而近场的长度将变长，两个关键位置之间的间距也将变小，并且灵敏度更高。换能器会变高，但分辨率会降低。相反，随着换能器直径减小，近场长度减小并且扩散角增加。超声波束将变得更加发散，并且两个关键位置之间的间隔也将增加。换能器的灵敏度会降低，而分辨率会更高。

图7c是两个探针的测试结果与实际水平值的比较。从图中可以看出，测试结果侧的探头的两个直径低于实际水平。系统错误是由系统的测量模型引起的。在错误分析之后应该提出后续校正方法来修改错误值。另外，因为两个探针的近场长度都大于8mm，所以延迟块用作次级测量以提高检测精度。然而，从测试结果可以看出，壁厚L = 8mm的测量值仍然大大偏离。从整体测量的角度来看，使用较大直径探针测量的结果比使用较小直径探针测量的结果相对接近真实水平。

图7d显示了分别使用两种探针检测四种不同壁厚下的液位的误差。从图中可以看出，当壁厚L = 8mm时，两个探针的测量误差达到约4mm~5mm。壁厚L≥25mm时，测量误差减小。当壁厚L = 25 mm时，探头误差值的两种不同尺寸已达到较小值。然而，从整体情况可以看出，较大直径探针的测量误差略低于小直径探针的测量误差。两个探针的测量误差通常保持在约3~5mm。
4。讨论
在该设计的超声波液位计测量中，首先通过测量液位附近的反射声波的变化特性来确定上临界位置和下临界位置。在测量模型中，液体介质和大气介质的阻抗是影响测量精度的主要因素。阻抗较大的液体介质，其反射声压变化很大，易于确定上下临界位置和液位; 在电阻较小的液体介质中，反射声压没有明显变化，难以固定上下临界位置和液位。因此，更高阻抗的液体介质更容易确定，

实验结果表明，通过两种不同直径尺寸的探头，反射声振幅的规律性相似。当小直径探头用于不同的壁厚时，反射声的差异一般大于大直径探头; 然而，液体的测量结果表明，由于不同直径探针在特殊测试环境中的不同物理特性，大直径探针的精度优于小探针，以平衡测试灵敏度和探针在一个过程中的分辨率。因此，在本文中关于超声波液体位置测量，探头直径的选择取决于壁厚和其他物理性质的测量，以更好地平衡其分辨率和灵敏度。
5。结论
在本研究中，在静态测量条件下，对于工业中的许多常见液体或混合液体，模型的测量精度小于±5 mm; 对于金属容器，试验厚度可达2~50 mm。因此，所提出的方法对于密封容器外的液位测量是有效的。