燃料油箱液位的测量应用及液位的误差值计算方式

抽象： 在本文中，我们考虑了燃料管理系统垂直通道中流体流动的数学建模问题。该系统具有垂直测量通道，在通道内具有液位计，用于固定通道中的自由表面液位。通过降低油箱中的燃油水平，油道中的油位降低。当通道中的燃料水平到达液位计时，发生液位计激活。因此，通道中的燃料水平决定了燃料箱中的燃料水平。垂直测量通道中的流体流动由抛物线型的非静止运动方程描述。对于动态建模，使用粘性不可压缩流体。流体流动被称为圆柱形通道的非平稳抛物线运动方程。我们通过平均通道半径的运动方程的项来得到问题的近似解。在Mathcad应用程序包中满足微分方程的解。随时间表示测量通道中燃料自由表面的位移和速度的图表。已确定燃料箱中液位的测量误差。提出了消除燃料使用液位计测量后误差的工程解决方案。
氧化剂罐和可燃罐的燃料流入火箭发动机的燃烧室。以预定比例同时供应燃料确保火箭发动机的有效操作。以预定比例的同步燃料输送使得火箭发动机的有效操作成为可能。有效的操作取决于罐中燃料液位的精确测量。为此，燃料箱具有燃料管理系统。该系统是一个垂直测量通道，通道内有液位计，用于固定通道中自由表面液位（图1）。
垂直通道和油箱是连通船。通过降低油箱中的燃油水平，油道中的燃油油位降低。当通道中的燃料水平到达液位计时，发生液位计激活。信号进入燃料管理系统。结果，燃料消耗变化。因此，通道中的燃料水平决定了燃料箱中的燃料水平。问题是燃料的自由表面在通道和罐中不重合。测量燃料水平时出错导致燃料消耗效率低下。结果，火箭发动机没有较佳运行，并且坦克具有“额外”量的燃料。

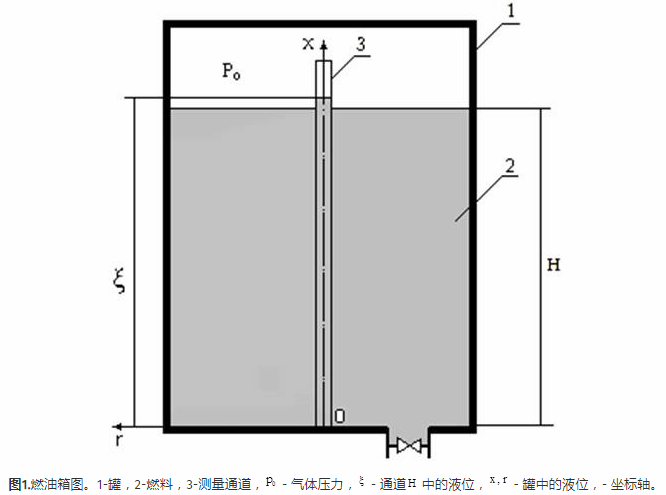
我们考虑了火箭燃料液位管理系统垂直通道内流体流动的数学模型问题。垂直测量通道中的流体流动由抛物线型的非静止运动方程描述。许多研究人员解决了非定常运动方程。在[讨论的问题1 - 3 ]可以被称为经典。文章[ 1 ]认为层流体在静止的圆柱形通道中流动。脉动运动见[ 2 ]。将周期运动的计算结果与实验数据进行比较。通过运算微积分求解运动方程。
在[ 5 ]中表明，在火箭发动机的实际使用中，氧化剂和可燃物的比例被打破。是什么导致节气门开度更大或更小。论文[ 6 ] 提出了一个非线性数学模型来模拟脉动流。控制方程通过复合方案进行数值求解，该方案结合了两步Lax-Wendroff方法和管道边界处特征方法的梯形积分版本。通过比较分析预测和实验结果，验证了数学模型和方法的有效性。
工作[ 7 ]显示由于瞬时阀门关闭导致的非牛顿流体的不稳定流动。通过数值方法求解适当的控制方程。四阶Runge-Kutta方案用于时间积分，中心差分方案用于空间导数离散化。为验证所提出的数学模型和数值解，与文献中的相应实验结果进行了比较。
在工作中[ 8 ]提出了用于模拟管道中非定常流动的特征方法（MOC）。然而，相对复杂的隐式（MOI）方法提供了无条件收敛和时空网格参数之间相互独立的优点。该研究结合了MOC和MOI来模拟管道非定常流动和水力瞬变过程。
论文[ 9 ]提出了研究圆形微管中不可压缩流体对突然的时间无关压降的响应的结果。使用拉普拉斯变换技术分析地获得问题的解决方案并且使用格子Boltzmann方法数值地获得该解决方案。
论文[ 10 ] 提出了一种温和弯曲管道中的稳定和不稳定流动，用于各种雷诺数的直接数值模拟。在文章[ 11 ]中，通过管道完全开发了不可压缩牛顿流体（原油）的脉冲流动，并使用有限元方法进行了建模和分析，并与基于解析解的结果进行了比较。通过叠加在恒定Poiseuille流上的周期性压力梯度产生流动。结果表明，基于有限元法的牛顿流体在非稳态条件下的解析解和数值解之间具有良好的一致性。
在文章[ 12 ]中，基于实验和数值模型分析了管道与非定常流动之间的动态相互作用。论文[ 13 ]提出了一种解决管网中流体流动一维模型的特征方法。
本研究的目的是建立火箭燃料液位测量系统垂直测量通道中液体流动的数学模型。

2.问题的数学表述
在初始时，油箱和通道中的燃油油位是相同的（）。圆柱形通道的自由上端位于油箱中的燃油液位上方，因此可以在该位置处将燃油从油箱流入通道。圆柱形通道的下部底部与罐的底部重合，并且燃料在罐和通道之间自由连通。在油箱中的燃料（）的自由表面上方并且通道保持恒定压力 （增压压力）。 

坦克中的燃料水平因法律而异。 - 降低油箱中的燃油速度。众所周知，罐和通道中的液位不重合。有必要在任意时间确定圆柱形通道中的液体水平。我们引入了一个坐标系，其开始位于圆柱形通道的下基部的中心。

作为流动的模型，使用粘性不可压缩流体在圆柱形通道中的非静止运动

3. 解决问题的方法

圆柱形通道中的平均燃料速度。将等式（1）的左侧和右侧乘以r。我们写下运动方程的各个项

我们使用公式（2）并以形式写出等式（1）（以下省略中等倾斜括号）

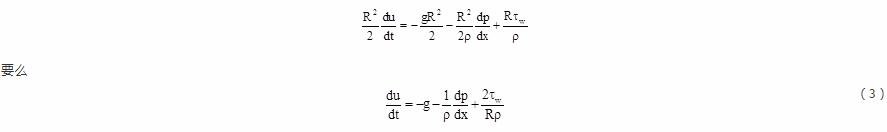
在圆柱形通道中选择一定距离的两个横截面的液体体积。记下压力和摩擦力的平衡。

然后，我们使用Darcy-Weisbach方程

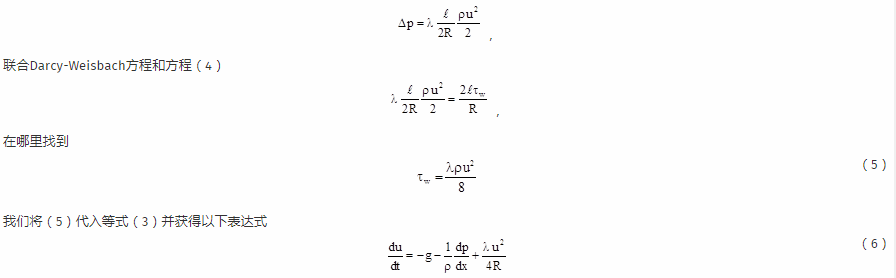
我们计算以下条件的压力梯度：压力从燃料自由表面上的增压压力线性减小到压力。压力梯度是
 

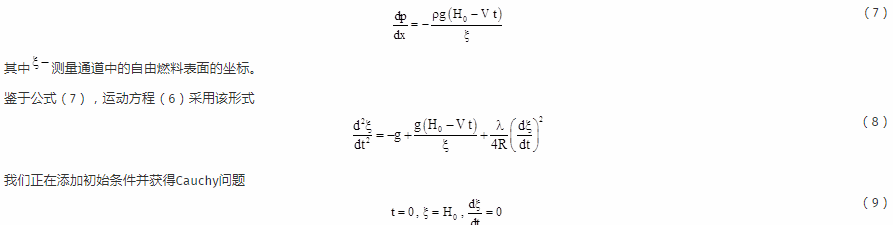
4. 结果
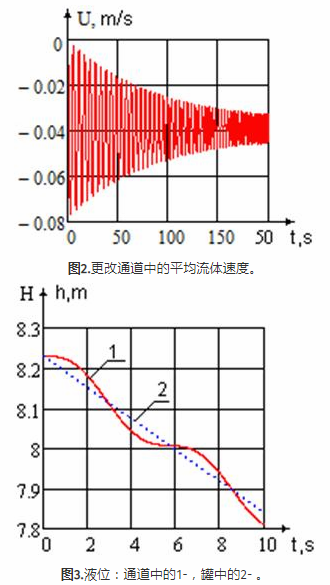
问题的进行数值解：，，，，。边界值问题的解决方案在包Mathcad应用程序中以数字方式给出。解决方案的结果显示在图表中（图2 - 图4）

5. 讨论

我们可以看到（图2），通道中流体的平均速度具有减小的振幅振荡。圆柱形通道中的液位相对于燃料箱中的液位波动（图3）。振荡的原因是通道中液柱的惯性。在初始时，液体具有非常大的加速度，这导致了很大的惯性力。因此，惯性力是导致通道中液体波动的原因。确定振荡过程的运动方程中的Summand是压力梯度。

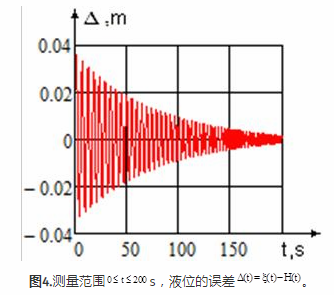
图表（图4）显示了测量液位与时间的误差。我们可以看到误差的大小是周期函数，其中振荡的幅度和周期随时间减小。在火箭飞行开始时观察到确定油箱中燃油水平的较大误差并达到该值△=0.035m。测量液位的误差不规律，使得难以调整软件中的错误。
注意，液位计可以以与罐中的燃料液位的实际位置的正偏差和负偏差的方式操作。在这种情况下，错误加倍。鉴于火箭直径的大小，我们谈论的是数百公斤燃料。

6. 结论
结果表明，水平液位计可能会提供虚假信息，具体取决于附着位置。错误不系统。实验研究耗时且昂贵。因此，数学实验是解决问题的较有效方法。任务是从液位计发出信号，对应于液体的实际液位。为此，液位计必须安装在功能的交叉点和。
应该注意的是，管理系统的垂直通道中的流体流动的数学模型没有考虑燃料箱火箭中的液体的波动和一些火箭设计特征。这项研究将在下一篇文章中完成。